In computer science, Hill-climbing is an optimization technique, used to find the best (or at least, a good enough) solution to a problem. It works by slowly improving a solution, until no better solution is reachable by gradual changes.

The general process of an optimization via Hill-Climbing is as follows:

  1. We get a random solution to our problem, which will be our initial solution.
  2. We check our current solution’s neighbours. A solution’s neighbour is another possible solution, which is identical, except for a small change. Depending on these neighbours, we may do different things:
    • If there’s one or more neighbours that are better than our current solution, we pick the best one as our new current solution and repeat the process (step 2).
    • If there isn’t any neighbour that is better than our current solution, we’ve reached an optimum (a local one, more details on that later). If we’re happy with the optimum, we stop the process here.

We can also represent the process with a graph like this one, where the Y axis represents the “goodness of a solution”, and higher is better.

If our random starting point is A, we would use its best neighbour and continue the process up the slope (hence the name “Hill Climbing”) until we get to the point where there isn’t any incremental change that would improve our solution (our Best Solution, in this case). Note that the graph is for illustrative purposes, a real problem would probably have more that two neighbours to each solution.

Strengths and Weaknesses of Hill Climbing

Hill climbing is a rather intuitive technique, whose main strength is that it doesn’t need to traverse every single solution to obtain an optimum, but rather starts in a random one and improves it gradually. Since the process depends on randomness, it execution isn’t consistent: we may be in our lucky day and start next door to the solution, or we may start in the solution that takes more steps to reach the optimum. However, it is almost certain that we’ll traverse less than we would if we verified each solution.

Local Optimums

However, our main strength also poses a big weakness. In our previous graph, if we (by chance) started in the solution B, we would traverse our best neighbours until we reach the “Good solution”, where no further improvement can be made by small steps. This solution, while one of the Best Solutions, is not THE best solution. Since Hill Climbing doesn’t traverse all possible solutions, it isn’t aware that there is an even better solution, and would return the Good Solution as an answer.

These good solutions are called “local optimum”. Doing Hill Climbing will end up in either a local optimum or in the global optimum (the BEST solution), depending on where it started.

To deal with this problem, we can perform another Hill Climbing from another random solution once we reached an optimum, and see if it ends on a better solution. On certain problems, we may be able to check if an optimum is the global optimum, which would further help us.

Note that some problems, under certain evaluations may enter into the “Convex” category, which means that they have only one optimum (the global one, of course). These problems are exempt from the local optimums issue.

Plateaus

Another problem that we may face are plateaus. We find ourselves in a plateau if there isn’t any neighbour better than our current state, but there are one or more neighbours which are as good as our current solution. In other words, we’re in a plateau if there’s nowhere better we can go, but we are not an optimum either (because there are neighbours with the same goodness).

Plateaus are problematic because a Hill Climbing algorithm won’t find any way to go, even if there are better solutions “beyond” the plateau, through one of the neighbours.

In this scenario, we can move to a random solution (either one of the current neighbours or a completely new one) to escape the plateau.

Example: The N-Queen Problem

As a demonstration of Hill Climbing, I will use it to solve the N-Queen problem. The N-Queen problem consists of the placement of N Queens on a NxN sized chessboard, so that no pair of queens can attack each other. In chess, a queen can move in every direction, vertically, horizontally or diagonally.

A solution to the N-Queen problem, on a 8×8 chessboard. Image from Geeks for Geeks

For simplicity purposes, we may rephrase the problem as:

Arranging N Queens on a N-sized chessboard, where every row has one and only one queen, every column has one and only one queen, and every diagonal has at most one queen.

So, for solving this problem, we can permanently assign a queen to each row. Now, each row has one queen, which can be on any of the N columns. With this consideration, we can further define how our program will handle the problem:

  • Every possible placement of the queens is handled as a “solution”, whether it satisfies the problem or not.
  • A solution’s neighbour is another solution on which one queen has changed its column, but all the others are in the same positions.
  • We evaluate the “goodness” of a solution with the number of collisions of it. Collisions are the amount of queen pairs that could attack each other, i.e. the amount of rows, columns or diagonals on the board that have more than one queen within them. Lower collisions is better.
  • In case we find ourselves in a plateau, we’ll switch to a random neighbour as our current state, and continue the process

The resulting program for solving the N-Queen problem with Hill Climbing is on this GitHub Repo. It is developed in C++, and uses the above considerations. Feel free to check it out, and identify the above considerations into the code.

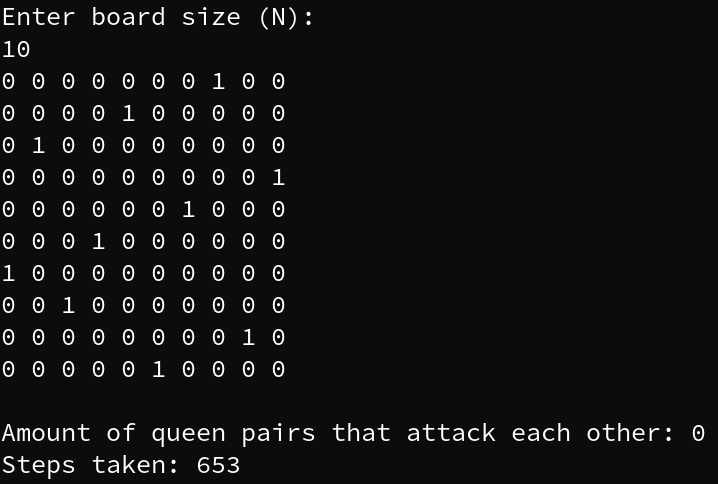
Result of executing the program several times, with a board size of 10×10. We can see how every execution may end up in a different (but optimal) solution, and takes a different amount of steps, due to the randomness at generating the initial state

So there you have it, this is the Hill Climbing technique for problem optimization, and how it can be used to solve a problem (in this case the N-Queen problem).

References

  1. GeeksforGeeks. (2022, October 25). N-Queen Problem | Local Search using Hill climbing with random neighbour. https://www.geeksforgeeks.org/n-queen-problem-local-search-using-hill-climbing-with-random-neighbour/
  2. Hill Climbing Algorithm in AI – Javatpoint. (n.d.). JavaTPoint. https://www.javatpoint.com/hill-climbing-algorithm-in-ai

Featured image by Alexis Fauvet on Unsplash